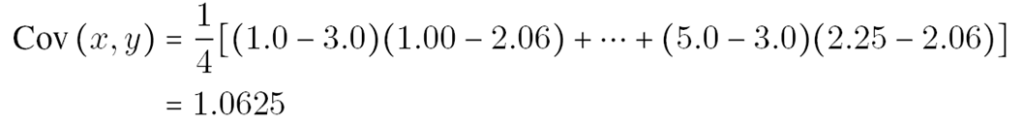Simple Linear Regression Model Solved Example in Machine Learning
Regression modeling is a process of determining a relationship between one or more independent variables and one dependent or output variable.
Example:
1. Predicting the height of a person given the age of the person.
2. Predicting the price of the car given the car model, year of manufacturing, mileage, engine capacity.
Simple Linear Regression Model
Assume that there is only one independent variable x. If the relationship between x (independent variable) and y (dependent or output variable) is modeled by the relation,
y = a + bx
then the regression model is called a linear regression model.
Problem Deninition:
Find a quadratic regression model for the following data:
| X | Y |
| 1 | 1 |
| 2 | 2 |
| 3 | 1.3 |
| 4 | 3.75 |
| 5 | 2.25 |
Solution:
Let the simple linear regression model be
y = a + bx
Steps to find a and b,
First, find the mean and covariance.
Means of x and y are given by,
The variance of x is given by,
The covariance of x and y, denoted by Cov(x, y)is defined as,
Now the values of a and b can be computed using the following formulas:
First, find the mean of x and y,
Next, find the Covariance between x and y,
Now find the variance of x,
Now, find the intercept and coefficients,
Therefore, the linear regression model for the data is,
Video Tutorial – Simple Linear Regression Model
Summary
This tutorial discusses the Simple Linear Regression Model Solved Example in Machine Learning. If you like the tutorial share it with your friends. Like the Facebook page for regular updates and YouTube channel for video tutorials.