ID3 Algorithm Decision Tree – Solved Example – Machine Learning
Problem Definition:
Build a decision tree using ID3 algorithm for the given training data in the table (Buy Computer data), and predict the class of the following new example: age<=30, income=medium, student=yes, credit-rating=fair
| age | income | student | Credit rating | Buys computer |
| <=30 | high | no | fair | no |
| <=30 | high | no | excellent | no |
| 31…40 | high | no | fair | yes |
| >40 | medium | no | fair | yes |
| >40 | low | yes | fair | yes |
| >40 | low | yes | excellent | no |
| 31…40 | low | yes | excellent | yes |
| <=30 | medium | no | fair | no |
| <=30 | low | yes | fair | yes |
| >40 | medium | yes | fair | yes |
| <=30 | medium | yes | excellent | yes |
| 31…40 | medium | no | excellent | yes |
| 31…40 | high | yes | fair | yes |
| >40 | medium | no | excellent | no |
Solution:
First, check which attribute provides the highest Information Gain in order to split the training set based on that attribute. We need to calculate the expected information to classify the set and the entropy of each attribute.
Video Tutorial ID3 Algorithm Decision Tree – Solved Example
The information gain is this mutual information minus the entropy:
The mutual information of the two classes,
Entropy(S)= E(9,5)= -9/14 log2(9/14) – 5/14 log2(5/14)=0.94
Now Consider the Age attribute
For Age, we have three values age<=30 (2 yes and 3 no), age31..40 (4 yes and 0 no), and age>40 (3 yes and 2 no)
Entropy(age) = 5/14 (-2/5 log2(2/5)-3/5log2(3/5)) + 4/14 (0) + 5/14 (-3/5log2(3/5)-2/5log2(2/5))
= 5/14(0.9709) + 0 + 5/14(0.9709) = 0.6935
Gain(age) = 0.94 – 0.6935 = 0.2465
Next, consider Income Attribute
For Income, we have three values incomehigh (2 yes and 2 no), incomemedium (4 yes and 2 no), and incomelow (3 yes 1 no)
Entropy(income) = 4/14(-2/4log2(2/4)-2/4log2(2/4)) + 6/14 (-4/6log2(4/6)-2/6log2(2/6)) + 4/14 (-3/4log2(3/4)-1/4log2(1/4))
= 4/14 (1) + 6/14 (0.918) + 4/14 (0.811)
= 0.285714 + 0.393428 + 0.231714 = 0.9108
Gain(income) = 0.94 – 0.9108 = 0.0292
Next, consider Student Attribute
For Student, we have two values studentyes (6 yes and 1 no) and studentno (3 yes 4 no)
Entropy(student) = 7/14(-6/7log2(6/7)-1/7log2(1/7)) + 7/14(-3/7log2(3/7)-4/7log2(4/7)
= 7/14(0.5916) + 7/14(0.9852)
= 0.2958 + 0.4926 = 0.7884
Gain (student) = 0.94 – 0.7884 = 0.1516
Finally, consider Credit_Rating Attribute
For Credit_Rating we have two values credit_ratingfair (6 yes and 2 no) and credit_ratingexcellent (3 yes 3 no)
Entropy(credit_rating) = 8/14(-6/8log2(6/8)-2/8log2(2/8)) + 6/14(-3/6log2(3/6)-3/6log2(3/6))
= 8/14(0.8112) + 6/14(1)
= 0.4635 + 0.4285 = 0.8920
Gain(credit_rating) = 0.94 – 0.8920 = 0.479
Since Age has the highest Information Gain we start splitting the dataset using the age attribute.
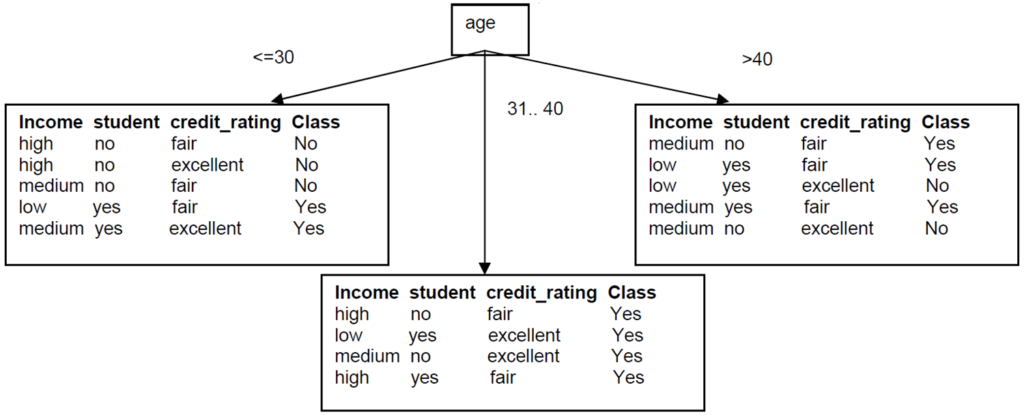
Since all records under the branch age31..40 are all of the class, Yes, we can replace the leaf with Class=Yes
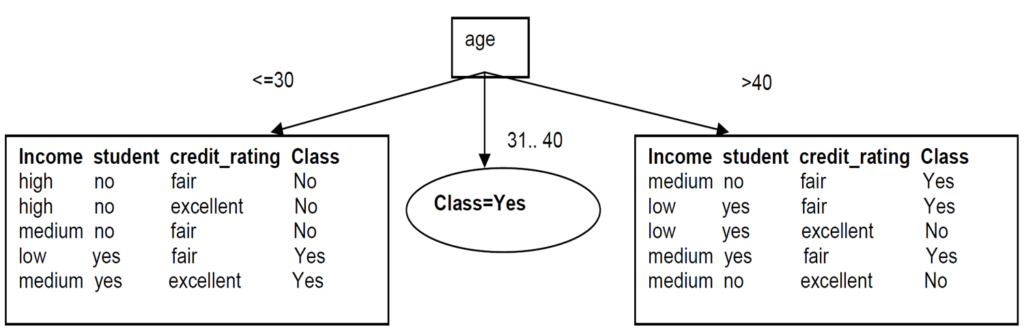
Now build the decision tree for the left subtree
The same process of splitting has to happen for the two remaining branches.

For branch age<=30 we still have attributes income, student, and credit_rating. Which one should be used to split the partition?
The mutual information is E(Sage<=30)= E(2,3)= -2/5 log2(2/5) – 3/5 log2(3/5)=0.97
For Income, we have three values incomehigh (0 yes and 2 no), incomemedium (1 yes and 1 no) and incomelow (1 yes and 0 no)
Entropy(income) = 2/5(0) + 2/5 (-1/2log2(1/2)-1/2log2(1/2)) + 1/5 (0) = 2/5 (1) = 0.4
Gain(income) = 0.97 – 0.4 = 0.57
For Student, we have two values studentyes (2 yes and 0 no) and studentno (0 yes 3 no)
Entropy(student) = 2/5(0) + 3/5(0) = 0
Gain (student) = 0.97 – 0 = 0.97
We can then safely split on attribute student without checking the other attributes since the information gain is maximized.
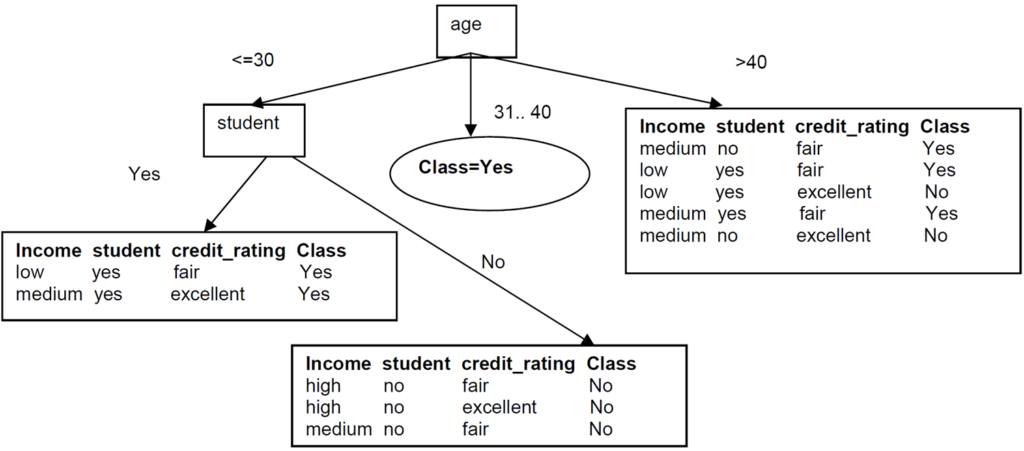
Since these two new branches are from distinct classes, we make them into leaf nodes with their respective class as label:
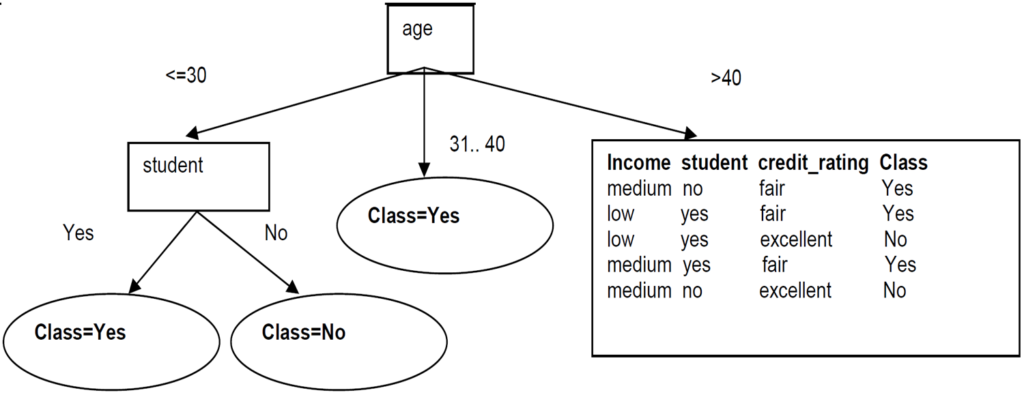
Now build the decision tree for right left subtree

The mutual information is Entropy(Sage>40)= I(3,2)= -3/5 log2(3/5) – 2/5 log2(2/5)=0.97
For Income, we have two values incomemedium (2 yes and 1 no) and incomelow (1 yes and 1 no)
Entropy(income) = 3/5(-2/3log2(2/3)-1/3log2(1/3)) + 2/5 (-1/2log2(1/2)-1/2log2(1/2))
= 3/5(0.9182)+2/5 (1) = 0.55+0. 4= 0.95
Gain(income) = 0.97 – 0.95 = 0.02
For Student, we have two values studentyes (2 yes and 1 no) and studentno (1 yes and 1 no)
Entropy(student) = 3/5(-2/3log2(2/3)-1/3log2(1/3)) + 2/5(-1/2log2(1/2)-1/2log2(1/2)) = 0.95
Gain (student) = 0.97 – 0.95 = 0.02
For Credit_Rating, we have two values credit_ratingfair (3 yes and 0 no) and credit_ratingexcellent (0 yes and 2 no)
Entropy(credit_rating) = 0
Gain(credit_rating) = 0.97 – 0 = 0.97
We then split based on credit_rating. These splits give partitions each with records from the same class. We just need to make these into leaf nodes with their class label attached:
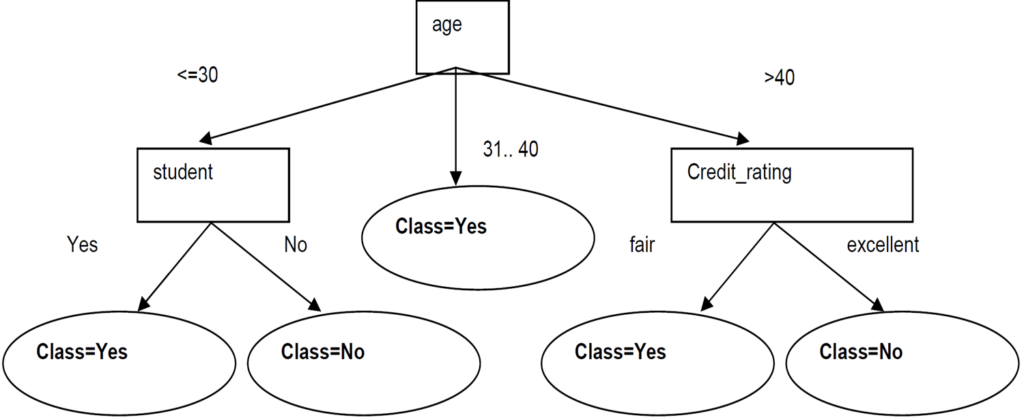
New example: age<=30, income=medium, student=yes, credit-rating=fair
Follow branch(age<=30) then student=yes we predict Class=yes
Buys_computer = yes
Summary:
This article discusses, ID3 Algorithm Decision Tree – Solved Example – Machine Learning. If you like the material share it with your friends. Like the Facebook page for regular updates and the YouTube channel for video tutorials.
